class: center, middle, inverse, title-slide .title[ # Case Selection ] .subtitle[ ## Multi-Method Research I ] .author[ ### <large>Jaye Seawright</large> ] .institute[ ### <small>IQMR 2025</small> ] .date[ ### June 26, 2025 ] --- class: center, middle <style type="text/css"> pre { max-height: 400px; overflow-y: auto; } pre[class] { max-height: 200px; } </style> --- ### Discovery vs. Confirmation --- ### Case Selection 1. Study the entire population. 2. Take a random sample. 3. Follow some rule for deliberate case selection. --- ### Choosing Cases - Case-selection rules: - Random sampling - Typical cases - Diverse cases - Extreme cases - Deviant cases - Influential cases - Most-similar cases - Contrast cases --- ### Typical Cases `$$\text{Typicality}_{i} = - \text{abs} [y_{i} - \text{E}(y_{i} | x_{1,i}, x_{2,i}, \ldots, x_{k,i})]$$` --- ### Extreme Cases `$$\text{Extremity}_{i} = \displaystyle| \frac{x_{i} - \bar{x}}{s} \displaystyle|$$` --- ### Deviant Cases `$$\text{Deviantness}_{i} = - \text{Typicality}_{i}$$` --- ### Influential Cases - Cook's distance is a statistical measure of how much the overall regression result would change if a given case is deleted. - A Cook's distance score of 1 or more usually is regarded as representing substantial influence. --- ### Influential Cases  --- ### Most-Similar Cases - Matching techniques are an automated way of finding most similar cases. --- ### Contrast Cases --- ### Measurement Error in `\(Y\)` `\(Y^{*}_{i} = Y_{i} + \delta_{Y, i}\)` Random Sampling --- ### Measurement Error in `\(Y\)` Typical/Deviant Cases: `\(e_{i} = Y_{i} - \mathbb{H}_{i, \cdot} Y + \delta_{Y, i}\)` --- ### Measurement Error in `\(Y\)` Influential Cases --- ### Measurement Error in `\(Y\)` Extreme Cases: `\(Y^{*}_{i} = Y_{i} + \delta_{Y, i}\)` --- ### Measurement Error in `\(Y\)` Most-Similar Cases Contrast Cases --- ### Measurement Error in `\(X\)` `\(X^{*}_{i} = X_{i} + \delta_{X, i}\)` Random Sampling --- ### Measurement Error in `\(X\)` Typical/Deviant Cases: `\(e_{i} = Y_{i} - X_{i} \hat{\beta}^{*} - \delta_{X, i} \hat{\beta}^{*}\)` --- ### Measurement Error in `\(X\)` Influential Cases --- ### Measurement Error in `\(X\)` Extreme Cases: `\(X^{*}_{i} = X_{i} + \delta_{X, i}\)` --- ### Measurement Error in `\(X\)` Most-Similar Cases Contrast Cases --- ### Confounding Variables `\(e_{i} = d_{i} + \gamma \tilde{Z_{i}}\)`, where `\(\tilde{Z_{i}} = Z_{I} - \text{E} (Z_{i} | X_{i})\)` Random Sampling --- ### Confounding Variables Typical/Deviant Cases: `\(e_{i} = d_{i} + \gamma \tilde{Z_{i}}\)` --- ### Confounding Variables Influential Cases --- ### Confounding Variables Extreme Cases: For confounders, extreme on `\(X\)` may be a good strategy. Extreme on `\(Y\)` maximizes: `\(\hat{Y}_{i} + d_{i} + \gamma \tilde{Z_{i}}\)` --- ### Confounding Variables Most-Similar Cases Contrast Cases --- ### Pathway Variables `\(W_{i} = \nu + \mu X_{i} + \omega_{i}\)` `\(Y_{i} = \alpha + \tau W_{i} + \sigma_{i}\)` Random Sampling --- ### Pathway Variables Typical/Deviant Cases: `\(e_{i} = \tau \omega_{i} + \sigma_{i}\)` --- ### Pathway Variables Influential Cases --- ### Pathway Variables Extreme Cases: `\(W_{i} = \nu + \mu X_{i} + \omega_{i}\)` Extreme on `\(Y\)` maximizes: `\(Y_{i} = \alpha + \tau W_{i} + \sigma_{i}\)` --- ### Pathway Variables Most-Similar Cases Contrast Cases --- ### Summary: Analytic Arguments | | Deviant | Influential | Ext. `\(X\)` | Ext. `\(Y\)` | | ------------- |:-------:| :----------:| :-------:| :-------:| | Error in `\(Y\)` | Good | Mixed | Poor | Good | | Error in `\(X\)` | Mixed | Mixed | Good | Poor | | Confounders | Mixed | Mixed | Good | Good | | Pathway | Good | Mixed | Good | Mixed | --- ### Propensity-Adjusted Extreme Cases ---  --- 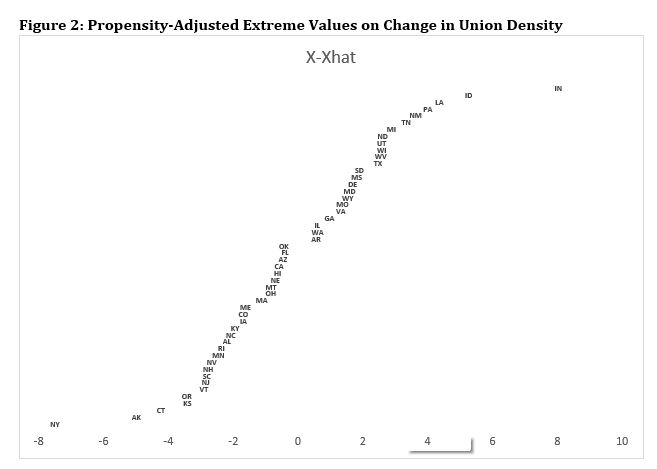 --- 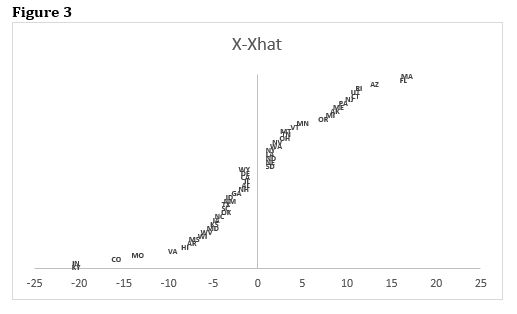 --- 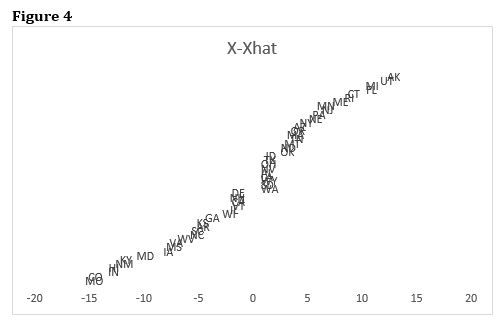 --- ### Confirmation <http://www.dagitty.net/dags.html> --- ### Herron and Quinn's Case Selection 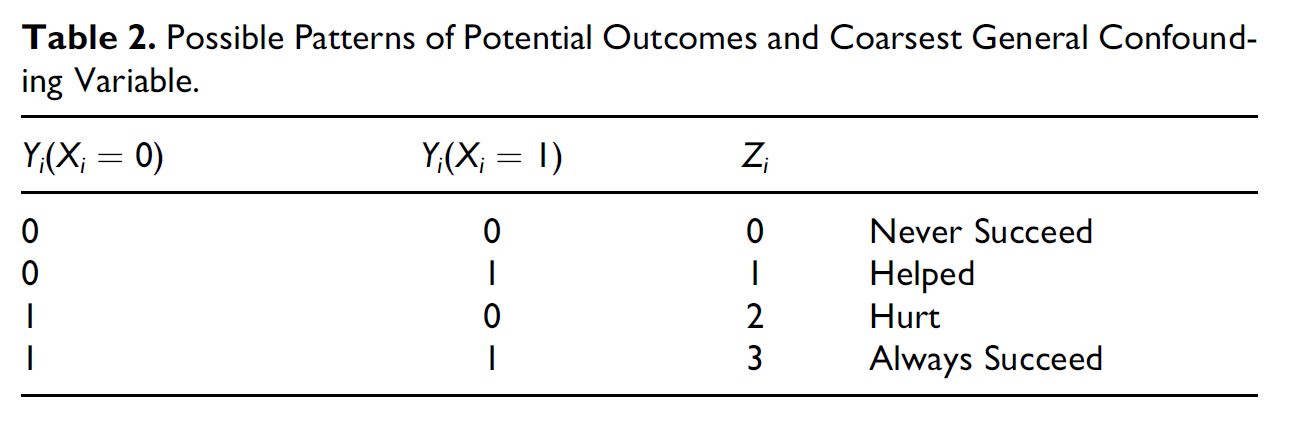 ---  --- ### Hands-On At [this website](https://jnseawright.github.io/practice-of-multimethod/Chapter-5.html), work through the exercise labeled *Case-selection Detective Work* vis-a-vis the choice of Yemen and Zimbabwe from the regression in the first exercise.